C++ programming for beginning programmers

Author: Chi-Hang Lam

These notes provide step-by-step instructions for the self-learning of the C++ programming language, without requiring any prior knowledge in computer programming. More than 60 downloadable example programs are included. They form part of a subject I teach at the Department of Applied Physics, the Hong Kong Polytechnic University. Information on more advanced C++ programming can be found, for example, at Wikibooks.

1 Overview of C++
    1.1 The simplest C++ program
    1.2 Execute C++ Program Online
    1.3 Mathemical functions
    1.4 Comments in a program
    1.5 Microsoft Visual Studio
    1.6 Using variables
    1.7 If and else
    1.8 Program indentation
    1.9 While loop
    1.10 Debugging approaches
2 C++ Fundamental Data Types
    2.1 Integer
    2.2 Floating point number
    2.3 Boolean
    2.4 Character
3 Identifier and Variable
    3.1 Identifier
    3.2 Variable Declaration
    3.3 Scope of Variable
4 Operators and Expressions
    4.1 Assignment operator (=)
    4.2 Arithmetic operators (+, - ,* , / , %)
    4.3 Compound assignment( +=, -=, *=, /=, %= )
    4.4 increase operator (++) and decrease operator (- -)
    4.5 Equality and Relational operators ( ==, !=, >, <, >=, <= )
    4.6 Logical operators ( !, &&, | | )
    4.7 Precedence of operators
5 Program control statements
    5.1 Simple statement and block of statements
    5.2 If and else
    5.3 While loop
    5.4 For loop
    5.5 Nested loops
    5.6 Further example
6 Functions
    6.1 Function Definition and Usage
    6.2 Value as Argument of function
    6.3 Returned value of function
    6.4 Mathematical Functions
    6.5 Variable as Argument of Function
7 Arrays
    7.1 Array Declaration and Usage
    7.2 Two-dimensional Arrays
    7.3 Further example
    7.4 Initialization of Array without specifying size
    7.5 Strings
    7.6 String operations
8 Input / Output
    8.1 Standard Output Stream (cout)
    8.2 Output manipulators
    8.3 Standard Input Stream (cin)
    8.4 Is input successful?
    8.5 File Output
    8.6 Graph Plotting
    8.7 File Input
9 Developing larger programs
    9.1 Ordering of functions
    9.2 Function declarations
    9.3 Multiple C++ source files
    9.4 C++ Header file and Include statement
    9.5 Namespace

Chapter 1
Overview of C++

1.1 The simplest C++ program

Below is the C++ source code in a file "simple.cpp" which calculates 12 ×14.

simple.cpp

#include <iostream>
using namespace std;

int main()
{
  cout << 12*14 << endl;
}

( simple.cpp )

Execution of the program gives the answer 168.

Explanation

12*14: an expression for 12 ×14. Multiplication is represented by the operator *.
cout: C++ standard output stream for printing to the computer screen
<<: output operator
endl: end-of-line character for finishing a printed line.
;: a semi-colon to mark the end of a C++ statement
{ , }: to mark the beginning and the end of a block of statement(s)
int main(): a declaration for a function called main. The main function is the entry point of a C++ program. It can give an integer (int) as a result.
#include <iostream>: to use a C++ header file called iostream, which enables printing to the screen
using namespace std: to use standard (std) pre-defined names

1.2 Execute C++ Program Online

The CodingGround website includes an Integrated Development Environment (IDE), which is a software assisting the development of C++.

To execute our program:

Using a web browser (e.g. firefox or internet explorer), enter the CodingGround website at http://www.tutorialspoint.com/compile_cpp_online.php.
In the source-code window in the middle, erase the original program and type our C++ program source codes.
Click Compile. No error message should appear in the Terminal window.
Click Execute. The answer 168 should appear in the Terminal window.

Alternatively, useful C++ IDE websites are cpp.sh and OnlineGDB.

1.3 Mathemical functions

Example:
Calculate √5, i.e. square root of 5

root.cpp

#include <iostream>
#include <math.h>
using namespace std;

int main()
{
  cout << sqrt(5.) << endl;
}

( root.cpp )

Explanation

sqrt: the square root mathematical function
#include <math.h>: to use a C++ header file called math.h, which enables the use of mathematical functions.
5.: the decimal point '.' specify that this is a floating point number.

Other mathematical functions include sin, cos, exp, log, pow, etc.

1.4 Comments in a program

Explanations about a program can be put as comments, e.g.

root2.cpp

/* root2.cpp 
   To compute the root of 5 
   written for Programming in Physics  */

#include <iostream>
#include <math.h>
using namespace std;

int main()
{
  cout << sqrt(5.) << endl; // root of 5
}

( root2.cpp )

Explanation

/* , */: mark the beginning and end of a multi-line comment
//: marks the rest of the line as a comment

Comments improves readability of a program. Better readability implies

easier to understand
easier to debug (i.e. remove errors)
easier to modify or improve (i.e. easier maintainance)

1.5 Microsoft Visual Studio

Microsoft Visual Studio is an Integrated Development Environment (IDE), which is a software assisting the development of C++ and other programs.

A free version called Visual Studio Enterprise 2017 is available from Microsoft. In the lectures, we will use this version. If you want to install at home, download from here. Click Visual Studio Enterprise 2017. Then follow the installation procedure. (Be careful: Make sure you install and use C++, NOT C#. They are different!)

To execute simple.cpp using Visual Studio 2017:

Start up Visual Studio
- In Windows, startup Visual Studio 2017.
- When used for the first time, you may be asked to create a microsoft account and sign-in.
Create a new Project/Solution called simple
- In the Visual Studio window, click File - - > New - - > Project - - > Empty project.
- Enter "simple" for the Name of the new project.
- Click Ok.
Create a C++ source code file called simple.cpp
- In Solution Explorer, right-click "Source Files", click "Add - - > New Item".
- In the Add New Item dialog box, select "C++ File (.cpp)". Enter "simple" for the Name of the source file and then click Add
Enter the source codes
- In the new "simple.cpp" tab, type in our C++ program source codes.
To keep output window from disappearing
A very annoying feature of visual studio is that the output window only remains on the screen for less than a second. To solve it,
either
- In the menu, click "Project - - > Simple Properties..."
- In the "Simple Properties Pages" window, click "Configuration Properties - - > Linker - - > System - - > SubSystem"
- In the "SubSystem" entry, click "Console (/SUBSYSTEM:CONSOLE)"
- click OK
or (not recommended)
Build the program
- Click BUILD - - > Build Solution. The message "Build succeeded" should appear in the Output window.
Run the program
- Click DEBUG - - > Start Without Debugging. A "cmd.exe" window should pop up and gives the answer 168.

1.6 Using variables

Example: Quadratic equation
Solve the equation

ax²+bx+c=0

(1.1)

for a=1, b=3 and c=−4.

The solution

−b ±

√

b² − 4 a c

(1.2)

can be computed using

quadratic1.cpp

// Solving ax^2 + bx + c = 0 for a=1, b=3, c=-4
#include <iostream>
#include <math.h>
using namespace std;

int main()
{
  cout << (-3.+sqrt(3.*3. -4.*1.*(-4.)))/(2.*1.) << endl;
  cout << (-3.-sqrt(3.*3. -4.*1.*(-4.)))/(2.*1.) << endl;
}

( quadratic1.cpp )

It outputs:
1
-4

Using variables, it can be improved to:

quadratic2.cpp

// Solving ax^2 + bx + c = 0 for a=1, b=3, c=-4
#include <iostream>
#include <math.h>
using namespace std;

double a, b, c; // declaring variables of type "double"

int main()
{
  a = 1.; // assigning value 1 to variable a
  b = 3.;
  c = -4.;

  cout << (-b + sqrt(b*b-4.*a*c))/(2.*a) << endl;
  cout << (-b - sqrt(b*b-4.*a*c))/(2.*a) << endl;
}

( quadratic2.cpp )

Explanation

Variable declaration: All variables must first be declared before use.
Varaible type: A variable type is specified in its declaration.
double: The double-precision floating point number variable type
Assignment statement: A variable can be assigned a value using the assignment operator '='. Further assignments overwrite old values.

Advantages of quadratic2.cpp

the C++ code (-b + sqrt(b*b-4*ac*))/(2*a) is directly related to Eq. (1.2), implying better readability
easier to modify the program for other problems, e.g. 2x² + 3x −4=0

Other important variable types include: int (integer), float (single-precision floating point number) char (character), and bool (boolean).

Introducing the determinant

D=b² − 4 a c

(1.3)

−b ±√D

(1.4)

the program can be alternatively written as

quadratic3.cpp

// Solving ax^2 + bx + c = 0 for a=1, b=3, c=-4
#include <iostream>
#include <math.h>
using namespace std;

double a, b, c; 
double D, x1, x2;

int main()
{
  a = 1.;
  b = 3.;
  c = -4.;
  D = b*b-4.*a*c; // determinant

  x1 = (-b + sqrt(D))/(2.*a); // 1st root
  x2 = (-b - sqrt(D))/(2.*a); // 2nd root

  cout << x1 << " " << x2 << endl; 
  // " " encloses a string of character(s)
}

( quadratic3.cpp )

It outputs: 1 -4

1.7 If and else

For a quadratic equation, solutions exist only under certain condition, i.e

If determinant D ≥ 0, solutions are given by Eq. (1.4)

This can be implemented using an if statement:

quadratic-if.cpp

// Solving ax^2 + bx + c = 0
#include <iostream>
#include <math.h>
using namespace std;

double a, b, c; 
double D, x1, x2;

int main()
{
  a = 1.;
  b = 3.;
  c = -4.;

  D = b*b-4.*a*c; // determinant

  if (D>=0){
    // only executed if expression is true
    x1 = (-b + sqrt(D))/(2.*a); // 1st root
    x2 = (-b - sqrt(D))/(2.*a); // 2nd root
    cout << x1 << " " << x2 << endl;
  }
}

( quadratic-if.cpp )

Alternatively, we can say:

If determinant D ≥ 0, solutions are given by Eq. (1.4), or else no solution exists.

This can be implemented using an if-else statement:

quadratic-if2.cpp

// Solving ax^2 + bx + c = 0
#include <iostream>
#include <math.h>
using namespace std;

double a, b, c; 
double D, x1, x2;

int main()
{
  a = 1.;
  b = 3.;
  c = -4.;
  
  D = b*b-4.*a*c; // determinant
  
  if (D>=0){
    x1 = (-b + sqrt(D))/(2.*a); 
    x2 = (-b - sqrt(D))/(2.*a); 
    cout << x1 << " " << x2 << endl;
  }else{
    cout << "no solution" << endl;
  }
}

( quadratic-if2.cpp )

The syntax of the if and if-else statements are

Syntax

if (condition){
  statement
}

Syntax

if (condition){
  statement
}else{
  statement
}

1.8 Program indentation

We should push the statements within a block enclosed by '{' and '}' by e.g. 2 spaces to the right.

Statements within a sub-block of a block should be further pushed by 2 more spaces, etc.

Proper indentation highlights the structure of a program and greatly enhances its readability.

1.9 While loop

Very often, we have to repeat similar actions many times, e.g. outputting 0,1,2, .. N−1 to the screen. The following program uses a direct approach for N=5:

noloop.cpp

#include <iostream>
#include <math.h>
using namespace std;

int main()
{
  cout << 0 << endl;
  cout << 1 << endl;
  cout << 2 << endl;
  cout << 3 << endl;
  cout << 4 << endl;
}

( noloop.cpp )

However, for large N, it is tedious to type in the program. The following version is slightly better because it can be entered by simple copy and paste actions:

noloop2.cpp

#include <iostream>
#include <math.h>
using namespace std;
int i;

int main()
{
  i = 0;   // i=0

  cout << i << endl; 
  i = i+1; // i=1

  cout << i << endl; 
  i = i+1; // i=2

  cout << i << endl; 
  i = i+1; // i=3

  cout << i << endl; 
  i = i+1; // i=4

  cout << i << endl;
  i = i+1; // i=5
}

( noloop2.cpp )

Explanation

i = i+1;: assign the value of i+1 to the variable i, i.e. i ← i+1. For example, if i is initially 0, after execution, i becomes 1.

Observing that the same statement "cout << i << endl; i = i+1;" is repeated 5 times, we can instead use a loop construction, e.g. the while loop:

whileloop.cpp

#include <iostream>
#include <math.h>
using namespace std;
int i;

int main()
{
  i = 0;
 
  while (i<5){ // repeat this block while i<5
    cout << i << endl; 
    i = i+1; 
  }
}

( whileloop.cpp )

Syntax

while (condition){
  statement
}

Tracing a program (i.e. running a program line-by-line)

Using OnlineGDB, type in the whileloop.cpp program. Then,

to start line-by-line program execution, click "Debug"
to set up a breakpoint, click the space on the left of the line number of "int main()". You will see a red dot.
to execute one line of the program, click "step over".
to 'watch' the value of a variable, in the "Display Expressions" tab, type "i". See value changes as you click "step over" a few times.

Advantages of Looping

the only means for repeatedly executing codes many times (e.g. 10¹⁰ times)
the codes to be repeated and the number of repetitions can be modified easily
more readable because the repetition is stated explicitly

Calculate the factorial n! of n defined by

n! = 1 ×2 ×3 .... ×n

(1.5)

The following program uses a direct approach

factorial1.cpp

// direct approach to calculate 5! (factorial of 5)
#include <iostream>
#include <math.h>
using namespace std;
int x;

int main()
{
  x = 1 * 2 * 3 * 4 * 5;
  cout << x << endl;
}

( factorial1.cpp )

which can be improved to

factorial1a.cpp

// direct approach to calculate 5! (factorial of 5)
#include <iostream>
#include <math.h>
using namespace std;
int x, i;

int main()
{
  x = 1;

  i = 1; x = x * i; // x=1  
  i = 2; x = x * i; // x=1.2
  i = 3; x = x * i; // x=1.2.3
  i = 4; x = x * i; // x=1.2.3.4
  i = 5; x = x * i; // x=1.2.3.4.5

  cout << x << endl;
}

( factorial1a.cpp )

and further improved to

factorial2.cpp

// direct approach to calculate 5! (factorial of 5)
#include <iostream>
#include <math.h>
using namespace std;
int x, i;

int main()
{
  i = 1;
  x = 1;

  x = x * i; i = i + 1; // x=1  i=2
  x = x * i; i = i + 1; // x=1.2  i=3
  x = x * i; i = i + 1; // x=1.2.3  i=4
  x = x * i; i = i + 1; // x=1.2.3.4  i=5
  x = x * i; i = i + 1; // x=1.2.3.4.5  i=6

  cout << x << endl;
}

( factorial2.cpp )

A better way is to use the while loop:

factorial-loop.cpp

// using while-loop to calculate n! (factorial of n)
#include <iostream>
#include <math.h>
using namespace std;
int n, x, i;

int main()
{
  n = 5;
  i = 1;
  x = 1;

  while (i<=n){
    x = x * i; 
    i = i + 1; 
  }
  cout << x << endl;
}

( factorial-loop.cpp )

1.10 Debugging approaches

Bugs and debugging

Mistakes in computer source codes are called bugs. The process of identifying and correcting the bugs is called debugging.

Types of bugs

Syntax errors (i.e. compiler errors, or build errors):: The grammatic rules of C++ is not followed, e.g. undeclared variable errors, errors due to a missing semi-colon, etc. (Easy)
Logical errors:: The program can be compiled and executed. However, due to logical or mathematical mistakes in the program, the results are incorrect. (Difficult!)

Logical errors

Can be difficult and time consuming to debug! Be patient! Don't despair! Don't blame your computer!
Good programming practices can minimize logical errors.

For example, the program below trys to calculate 5! but outputs 8 instead. Why?

factorial-bug.cpp

// using while-loop to calculate n! (factorial of n)
#include <iostream>
#include <math.h>
using namespace std;
int n, x, i;

int main()
{
  n = 5;
  i = 1;
  x = 1;

  while (i<=n){
    x = x * i; 
    i = i + i; 
  }
  cout << x << endl;
}

( factorial-bug.cpp )

Common debugging approaches for logical errors

Inspection, i.e. read the source code many times carefully
Dry running, i.e. imitating the execution by doing the calculations by hand
Outputting intermediate values of the variables to obtain more clues
Tracing the execution and examining intermediate variables using a debugger to obtain more clues
Last resort: forget your buggy program. Start all over again

Outputting intermediate values

For example, statements for outputting intermediate values are added for debugging purpose:

factorial-debug.cpp

// using while-loop to calculate n! (factorial of n)
#include <iostream>
#include <math.h>
using namespace std;
int n, x, i;

int main()
{
  n = 5;
  i = 1;
  x = 1;

  while (i<=5){
    x = x * i;   
    cout << x << endl; // for debugging
    i = i + i;   
    cout << i << endl; // for debugging
  }
  cout << x << endl;
}

( factorial-debug.cpp )

Tracing a program with Visual C++

The simplest way of tracing is executing it step by step repeatedly, e.g. for Visual Studio,

clicking Debug - - > Step Over
or, pressing F10

Values of active variables are shown in an "Autos" window after every step of execution.

Chapter 2
C++ Fundamental Data Types

2.1 Integer

For Visual C++,

Type	Description	Storage size	Allowed values

unsigned int	unsigned (positive) integer	32 bits (4 bytes)	0 .. 4294967295 (2³²−1)
int	signed integer	32 bits (4 bytes)	-2147483648 .. 2147483647

(Other compilers may adopt different storage size and allowed values)

The following program outputs 100 1 1 -1 2 2 3.

integer.cpp

// type casting and integer division
#include <iostream>
#include <math.h>
using namespace std;
int n1, n2, n3, n4, n5, n6, n7;

int main()
{
  n1 = 100; // integer constant assigned to n1
  n2 = 1.5; // implicit type casting  (avoid!)
  n3 = (int) 1.5; // explicit type casting -> 1
  n4 = (int) -1.5; // explicit type casting -> -1 
  n5 = 5/2; // integer division -> 2  (avoid unless needed!)
  n6 = (int) (5./2.); // floating point division & type casting -> 2
  n7 = (int) (5./2.+0.5); // do 5./2.+0.5 & type casting -> 3

  cout << n1 << ' ' << n2 << ' ' << n3  << ' ';
  cout << n4 << ' ' << n5 << ' ' << n6  << ' ' << n7 << endl;
}

( integer.cpp )

Explanation

The type casting operator (int) converts floating point numbers to int type. Fractions are simply truncated (i.e. dropped).
Avoid implicit type casting to int variables because the truncation is not obvious to the reader (i.e. poor readability).
Avoid integer division unless it is necessary.

Overflow error occurs when required value is outside the allowed range. No error message will be given, but results will be incorrect (wrapped around).

integer-overflow.cpp

// demonstrate overflow error of int variables
#include <iostream>
#include <math.h>
using namespace std;
int n, n1, n2;

int main()
{
  n = 2147483647;
  n1 = n + 1; // value too large, overflow occurs
  n2 = -n -2; // value too negative, overflow occurs
  cout << n << ' ' << n1 << ' ' << n2 <<  endl;
}

( integer-overflow.cpp )

It incorrectly outputs 2147483647 -2147483648 2147483647 (correct result: 2147483647 2147483648 -2147483649).

2.2 Floating point number

A single precision floating point number with 32 bits is expressed as

x = (−1)^s ×m ×2^e−127

(2.1)

Explanation

s (1 bit): Sign bit, s = 0 or 1
e (8 bits): Exponent, e = 0 .. 255
m (23 bits): Significand, m = 1.00000000000000000000000 .. 1.11111111111111111111111 (in binary)

Example: Singe precision floating point number
A single precision floating point number x is represented by s=1, e=130 (in decimal), and m=1.1101 (in binary). Calculate x in decimal form.

Answer:

m

=

1 + 1/2 + 1/4 + 0/8 + 1/16 = 1.8125

x

=

(−1)¹ ×1.8125 ×2^130−127 = −14.5

The maximum expressible value (overflow threshold) is about x_max=2¹²⁸. Overflow Error occurs when a value is outside [−x_max, x_max]. Then, NaN (not a number) results.
The minimum non-zero expressible value (underflow threshold) is about x_min=2⁻¹²⁷. Underflow occurs when a value is within [−x_min, x_min]. Then, 0 results.
Numbers in computers have finite precisions. Further digits are automatically rounded off.
The machine epsilon (machine precision) ϵ is the smallest value so that 1+ϵ is not rounded off to 1. Here, ϵ ≅ 2⁻²⁴

Typical properties of single and double precision floating point numbers are

Type	Precision	Storage	Machine epsilon	Overflow threshold	Underflow threshold

float	Single	32 bits	2⁻²⁴ ≈ 5.96×10⁻⁸	2¹²⁸ ≈ 3.40×10³⁸	2⁻¹²⁶ ≈ 1.18×10⁻³⁸
double	Double	64 bits	2⁻⁵³ ≈ 1.11×10⁻¹⁶	2¹⁰²⁴ ≈ 1.79×10³⁰⁸	2⁻¹⁰²² ≈ 2.23×10⁻³⁰⁸

double.cpp

// double precision floating point numbers
#include <iostream>
#include <math.h>
using namespace std;
double x1, x2, x3, x4, x5, x6;

int main()
{
  x1 = 6.022e23; // floating point constant assigned to x1
  x2 = 1.e300 * 1.e100; // overflow -> Nan, inf, or ..
  x3 = 1.e-300 / 1.e100; // underflow -> 0
  x4 = 1. + 1e-8; // -> 1.00000001 but will be displayed as 1
  x5 = (1. + 1e-8) -1.; // -> 1e-8, as expected
  x6 = (1. + 1e-16) -1.; // -> 0, due to machine precision error

  cout << x1 << ' ' << x2 << ' ' << x3  << ' ';
  cout << x4 << ' ' << x5 << ' ' << x6  << endl;
}

( double.cpp )

The above program outputs 6.022e023 1.#INF 0 1 1e-008 0

Explanation

6.022e23 denotes the scientific notation 6.022×10²³
When outputting, a copy of the number is displayed after further rounding off. The original variable (e.g. x4) is however unaffected.

2.3 Boolean

The data type for a boolean value is

Type	Description	Storage size	possible values

bool	Boolean	8 bits (1 bytes)	0, 1

Although only 1 bit is needed, 1 byte is used (i.e. 7 bits wasted) for better efficiency.

Two constants 'true' and 'false' are pre-defined as 1 and 0.

2.4 Character

Characters, including letters, digits, and symbols are numbered using the ASCII (American Standard Code for Information Interchange) code.

(which have been generalized to extended ASCII code and unicode)

The data type for a character is

Type	Description	Storage size

char	character	8 bits (1 bytes)

Chapter 3
Identifier and Variable

3.1 Identifier

An identifier is a name used to describe variables, functions, constants and other items.

An Identifier

must begin with a letter or underscore.
can be followed by letters(A-Z,a-z), digits(0-9), or underscore( _ )
are case sensitive, e.g. " int x,X; " declares 2 different variables.
must not be a reserved word

C++ reserved words are

  auto   const     double  float  int       short   struct   unsigned
  break  continue  else    for    long      signed  switch   void
  case   default   enum    goto   register  sizeof  typedef  volatile
  char   do        extern  if     return    static  union    while
  
  asm         dynamic_cast  namespace  reinterpret_cast  try
  bool        explicit      new        static_cast       typeid
  catch       false         operator   template          typename
  class       friend        private    this              using
  const_cast  inline        public     throw             virtual
  delete      mutable       protected  true              wchar_t
  
  and      bitand   compl   not_eq   or_eq   xor_eq
  and_eq   bitor    not     or       xor

3.2 Variable Declaration

A variable declaration has the syntax:

[modifier] <type> <variable identifier> [ = <initial value>];

where <..> denotes an argument and [..] indicates an optional argument

e.g.

quadratic-declaration.cpp

// Solving ax^2 + bx + c = 0
#include <iostream>
#include <math.h>
using namespace std;

const double a=1., b=3., c=-4.; // constant variables 
                                // & initial values
double D, x1, x2;

int main()
{
  D = b*b-4.*a*c; // determinant

  if (D>=0){
    x1 = (-b + sqrt(D))/(2.*a); // 1st root
    x2 = (-b - sqrt(D))/(2.*a); // 2nd root
    cout << x1 << " " << x2 << endl;
  }
}

( quadratic-declaration.cpp )

Explanations

const is a modifier
Constants (or constant variables) declared with const cannot be reassigned to other values.
Using const is not strictly necessary in most cases, but enhances readability and reliability.

3.3 Scope of Variable

The scope of a variable is the range in the program where it can be referenced (i.e. used).

Global variables are declared outside any functions and can be referenced anywhere in the program.

Local variables are declared inside a block and can be referenced only within the block.

A declaration can be put anywhere in the program before it is first used.

quadratic-scope.cpp

// Solving ax^2 + bx + c = 0
#include <iostream>
#include <math.h>
using namespace std;

const double a=1., b=3., c=-4.; 

int main()
{
  double D = b*b-4.*a*c; // determinant (local variable)

  if (D>=0){
    double x1 = (-b + sqrt(D))/(2.*a); // 1st root (local variable)
    double x2 = (-b - sqrt(D))/(2.*a); // 2nd root (local variable)
    cout << x1 << " " << x2 << endl;
  }
}

( quadratic-scope.cpp )

Advantages of local variables

allow variables of the same name in different blocks
indicate the scope (local or global) of variables and enhances readability
decrease memory usage because memory is released after finishing a block

Chapter 4
Operators and Expressions

4.1 Assignment operator (=)

To assign a value b to variable a, write

a = b;

To assign a value c to variables a and b, write

a = b = c;

4.2 Arithmetic operators (+, - ,* , / , %)

+	addition
-	subtraction
*	multiplication
/	division
%	modulo, i.e. remainder

4.3 Compound assignment( +=, -=, *=, /=, %= )

A compound assignment statement modifies the value of a variable by operating on its value,

e.g. to increase a by 1, write

a += 1;

which is equivalent to

a = a + 1;

e.g. to replace a by its product with b, write

a *= b;

which is equivalent to

a = a * b;

4.4 increase operator (++) and decrease operator (- -)

The increase operator, ++, increases the value of a variable by 1. The following statements are equivalent:

a = a + 1;

a +=1 ;

a++;

++a;

It is similar for the decrease operator.

4.5 Equality and Relational operators ( ==, !=, >, <, >=, <= )

These operators give Boolean values (i.e. true or false):

==	equal to
!=	not equal to
>	greater than
<	less than
>=	greater than or equal to
<=	less than or equal to

e.g.

if (a==b) { ... }

4.6 Logical operators ( !, &&, | | )

C++ logical operators for Boolean values are

!	not
&&	and
\| \|	or

e.g. the Boolean expression 0 ≤ x < 3.1416 can be written as

if ( (0 <= x) && (x < 3.1416) ) { ... }

4.7 Precedence of operators

Some operation has higher precedence (i.e. higher priority) and will be executed before others. Operations of the same precedence will be executed from the left to the right, e.g.

a = 1 + 2 * 3;

is equivalent to

a = 1 + (2 * 3);

e.g.

a = 5. / 3. / 8.;

is equivalent to

a = (5. / 3.) / 8.;

The order of precedence of some C++ operators, starting from the highest, is

* / %

+ -

< > <= >=

== !=

| |

It is a good practice to add parenthesis () to enforce and make explicit the desired order of execution.

Chapter 5
Program control statements

5.1 Simple statement and block of statements

A C++ statement can either be

a simple statement, i.e. a simple instruction ending with a semicolon,
or, a block of statements separated by semicolons and enclosed by { }

5.2 If and else

The syntax of the if and if-else statements are

Syntax

if (condition)
  statement

Syntax

if (condition)
  statement
else
  statement

where a statement can be a simple statement or a block.

Nested if-else statement: A statement in an if or if-else construction is itself be an if or if-else statement, e.g.

Syntax

if (condition){
  if (condition)
    statement
}else{
  if (condition)
    statement
  else
    statement
}

Consider again the quadratic equation

ax²+bx+c=0

(5.1)

For a < > 0, it has solutions,

−b ±

√

b² − 4 a c

for D > 0

(5.2)

Otherwise, it has solution,

x = −

for b < > 0

(5.3)

quadratic-if3.cpp

// Solving ax^2 + bx + c = 0
#include <iostream>
#include <math.h>
using namespace std;

const double a=1., b=3., c=-4.; 

int main()
{
  if (a != 0){ 
    // quadratic equation
    double D = b*b-4.*a*c; 
    if (D >= 0){
      double x1 = (-b + sqrt(D))/(2.*a); // 1st root
      double x2 = (-b - sqrt(D))/(2.*a); // 2nd root
      cout << x1 << " " << x2 << endl;
    }
  }else{
    // linear equation
    if (b != 0){
      double x1 = - c / b;
      cout << x1 << endl; // root
    }
  }
}

( quadratic-if3.cpp )

5.3 While loop

5.4 For loop

A loop using a counter typically has an initialization, a condition, and an increment, e.g.

int i=0; // initialization

while (i < N) { // condition

double m = i;

M += m;

++i; // increment

}

It can be conveniently written using a for loop.

Syntax

for (initialization; condition; increment)
  statement

The statement forms the loop body.

Explanation

initialization: executed when first entering the loop
condition: checked before every execution of the loop body. The loop body will only be executed if the condition is true, otherwise the loop ends.
increment: executed after every execution of the loop body.

The total mass problem can be solved by the following equivalent program

balls_mass_for.cpp

// total mass of N balls
#include <iostream>
#include <math.h>
using namespace std;

const int N = 100; // no. of balls

int main()
{
  double M=0;      // partial sum, which becomes total mass

  for (int i=0; i<N; ++i){   // repeat N times
    double m  = i; // m_i (mass of i-th ball)
    M += m ;       // i.e. M=M+m ( add m_i to partial sum )
  }
  cout << M << endl;
}

( balls_mass_for.cpp )

5.5 Nested loops

Inside a loop, the content can itself be a loop. This is called a nested loop.

Example: Two dice
List all 36 possible outcomes when rolling two dice

dice.cpp

// Possible outcomes when rolling 2 dice with nested loops
#include <iostream>
#include <math.h>
using namespace std;

const int N = 6; // no. of faces of a die

int main()
{
  // outer loop
  for (int i=1; i<=N; ++i){

    // inner loop
    for (int j=1; j<=N; ++j){
      cout << i << ' ' << j << endl;
    }

  }
}

( dice.cpp )

Program output: dice.txt

5.6 Further example

Example: Prime number
Check if the number n=137891 is a prime number or a composite number.

If n is divisible by some p ∈ [2,n−1], then n is a composite number, otherwise it is a prime number.

Algorithm (i.e. method of calculation):

Consider each p ∈ [2,n−1] until all values considered or n proven composite.
- if n is divisible by p, n is proven composite.

prime.cpp

// check if a number n is prime or composite
#include <iostream>
#include <math.h>
using namespace std;

const int n=137891; 

int main()
{
  bool composite = false; // not proven composite yet

  // loop over all p in [2,n-1] while not proven composite
  for (int p=2; (p < n) && (!composite); ++p){ 

    if (n % p == 0) {        // divisible ?
      composite = true;      // n is composite
      cout << p << ' ' << n/p << endl;
    }
  }

  if (composite)
    cout << "composite" << endl;
  else
    cout << "prime"<< endl;
}

( prime.cpp )

Program output:

13 10607

composite

Chapter 6
Functions

6.1 Function Definition and Usage

Some segments of codes may be repeated a few times in a program, e.g.

Example: Functions
Calculate the surface area and volume of spheres of radii 1, 3, and 7.

SphereProperties.cpp

// calculate and output the surface area and volume 
// of spheres of radii 1, 3, and 7
#include <iostream>
#include <math.h>
using namespace std;

const double pi = 3.1416;

double r, area, volume;

int main()  
{
  r=1.;
  area = 4.*pi*r*r; 
  volume = 4./3.*pi*r*r*r;
  cout << r << ' ' << area << ' ' << volume << endl;
  
  r=3.;
  area = 4.*pi*r*r; 
  volume = 4./3.*pi*r*r*r;
  cout << r << ' ' << area << ' ' << volume << endl;
  
  r=7.;
  area = 4.*pi*r*r; 
  volume = 4./3.*pi*r*r*r;
  cout << r << ' ' << area << ' ' << volume << endl;
}

( SphereProperties.cpp )

Repeated codes can be defined in a function. Applying 'function' in C++ involves:

Defining the function once with the desired codes
Calling (i.e. using) the function one or more times to execute the codes.

Using function, the above program becomes

SphereProperties-function.cpp

// Properties of spheres of radii 1, 3, and 7 using function
#include <iostream>
#include <math.h>
using namespace std;
const double pi = 3.1416;

double r;

void Sphere() // defining a function
{
  double area, volume; // variables local to this function
  area = 4.*pi*r*r; 
  volume = 4./3.*pi*r*r*r;
  cout << r << ' ' << area << ' ' << volume << endl;
}

int main()  
{
  r=1.;
  Sphere(); // calling the function, i.e. calling point
  
  r=3.;
  Sphere(); // calling the function, i.e. calling point
  
  r=7.;
  Sphere(); // calling the function, i.e. calling point
}

( SphereProperties-function.cpp )

Syntax of Function Definition

void <function name>()
{
  statement
}

Syntax of Calling a Function

<function name>()

Explanation

The statement inside the function definition is the function's body.
A function must be defined before it can be called.
When a function is called by writing <function name>() , it is as if the function's body is 'inserted' into the calling point (i.e. where it is called). (See function-inserted.cpp .)

Advantages of functions

Important way to repeat identical or similar code segments
Function name tells the purpose of a code segment and enhance readability (i.e. may also be helpful to defined non-repeating codes as function)
Breaking a large block into smaller blocks (usually within a page long) to enhance readability.

6.2 Value as Argument of function

In the example above, the radius is passed (i.e. supplied) to the function using the global variable r. A much better approach is passing r as a function argument (i.e. function parameter), e.g.

function-argument.cpp

// Properties of spheres of radii 1, 3, and 7
// using function argument
#include <iostream>
#include <math.h>
using namespace std;
const double pi = 3.1416;

void Sphere(double r) // r is an argument
{
  double area, volume;
  area = 4. * pi * r * r; 
  volume = 4./3. * pi * r * r * r;
  cout << r << ' ' << area << ' ' << volume << endl;
}

int main()  
{
  Sphere(1.);
  Sphere(3.);
  Sphere(7.);
}

( function-argument.cpp )

Syntax : Function Definition with Arguments

void <func. name> ( [<variable type> <variable name>] [, ...] ){
  statement
}

A function can have multiple arguments, e.g.

function-argument2.cpp

// Properties of spheres of radii 1, 3, and 7
// with densities 7.87, 8.96, 11.36 respectively
// using function arguments
#include <iostream>
#include <math.h>
using namespace std;
const double pi = 3.1416;

void Sphere(double r, double rho) // r=radius, rho=density
{
  double area, volume, mass;
  area = 4. * pi * r * r; 
  volume = 4./3. * pi * r * r * r;
  mass = rho * volume;
  cout << r << ' ' << area << ' ' << volume << ' ' << mass << endl;
}

int main()  
{
  Sphere(1., 7.87);
  Sphere(3., 8.96);
  Sphere(7., 11.36);
}

( function-argument2.cpp )

6.3 Returned value of function

A C++ function can be similar to a mathematical function, e.g.

Example: The Square Function
Calculate 1.5^2 by defining a function called sqr

sqr.cpp

#include <iostream>
#include <math.h>
using namespace std;

double sqr(double x) // function returns a value of type double
{
  double y = x*x; 
  return y;  // returned value
}

int main()
{
  cout << sqr(1.5) << endl; // calling function sqr with parameter 1.5
}

( sqr.cpp )

Example: More General One-to-one Function
Calculate f(x) = 1.2 x² − 3 x + 1 for x=0.1

function.cpp

#include <iostream>
#include <math.h>
using namespace std;

double f(double x) // function return a value of type double
{
  double y = 1.2 * x*x - 3.*x + 1.; 
  return y;  // returned value
}

int main()
{
  cout << f(0.1) << endl; // calling function f with parameter 0.1
}

( function.cpp )

A mathematical function f(x) returns (i.e. gives) a value.

A C++ function can also return a value. The expression <function name>() at the called point is substituted by the returned value.

Syntax : Function Definition with Returned Value

<return type> <func. name> ( [<vari. type> <vari. name>] [,...] ){
  statement
}

Explanation

the "return <variable name>" statement specifies which value is the function's returned value. It also end execution of the function, and program continues again from after the calling point.

Example: Returned values of Functions
Calculate the total mass of spheres of radii 1, 3, and 7 and densities 7.87, 8.96, 11.36 respectively.

function-return.cpp

// Total mass of spheres of radii 1, 3, and 7
// with densities 7.87, 8.96, 11.36 respectively
// using function arguments and returned value
#include <iostream>
#include <math.h>
using namespace std;
const double pi = 3.1416;

double SphereMass(double r, double rho) // value of type double 
                                        // will be returned
{
  double volume = 4./3. * pi * r * r * r;
  double mass = rho * volume;
  return mass; // mass (not volume) as returned value of function;
}

int main()  
{
  double m1 = SphereMass(1., 7.87); // returned value of SphereMass() assigned to m1
  double m2 = SphereMass(3., 8.96);
  double m3 = SphereMass(7., 11.36);
  cout << m1 + m2 + m3 << endl;
}

( function-return.cpp )

6.4 Mathematical Functions

Many useful mathematical functions are pre-defined, including

Function	Declaration	Description

sqrt(x)	double sqrt(double x);	square root
pow(x,y)	double pow(double x, double y);	x raised to power y, i.e. x^y
exp(x)	double exp(double x);	exponentiation
log(x)	double log(double x);	natural logarithm
abs(x)	int abs(int x);	absolute value
fabs(x)	double fabs(double x);	absolute value
floor(x)	double floor(double x);	truncate to whole number (not rounding)

sin(x)	double sin(double x);	sine
cos(x)	double cos(double x);	cosine
tan(x)	double tan(double x);	tangent
asin(x)	double asin(double x);	arc-sine
acos(x)	double acos(double x);	arc-cosine
atan(x)	double atan(double x);	arc-tangent

(trigonometric functions assume parameters in radian)

6.5 Variable as Argument of Function

A function can return more than one value by

using global variables (not recommended)
using variables as arguments to store and return values

function-reference.cpp

#include <iostream>
#include <math.h>
using namespace std;
const double pi = 3.1416;

void GetSphereProp(double r, double &a, double &v) 
// r represents the value 2.
// a represents the variable Area
// v represents the varaible Volume
{
  a = 4. * pi * r * r;        // assigning to variable Area
  v = 4./3. * pi * r * r * r; // assigning to variable Volume
}

int main()  
{
  double radius, Area, Volume;
  radius = 2.;
  GetSphereProp(radius , Area, Volume);
  // value of the variable radius passed to function
  // the variables Area, Volume passed to function
  cout << Area << ' ' << Volume << endl;
}

( function-reference.cpp )

Explanation

&<variable> gives the reference (i.e. memory address) of the variable.
reference as an argument of a function means that the argument is the variable itself (rather than its value).

Chapter 7
Arrays

7.1 Array Declaration and Usage

A sequence in mathematics is an ordered list of numbers. For example, consider a sequence {1, 4, 9, 16, 25, 36}

The sequence has 6 entries (i.e. members)
The entries are numbered from 0 to 5 (not from 1 to 6 ! )
e.g. entry 0 equals 1
e.g. entry 4 equals 25

entry	0	1	2	3	4	5
value	1	4	9	16	25	36

The above sequence can be stored in an integer array, e.g.

integer_array.cpp

#include <iostream>
#include <math.h>
using namespace std;

int main()
{
  int x[6] = {1, 4, 9, 16, 25 ,36}; 
    // declare an int array of 6 entries
    // and initialize it by the given sequence

  cout << x[0] << ' ' << x[4] << endl;
    // output entries 0 and 4
}

( integer_array.cpp )

To declare an array, follow

Syntax

<type> <array name> [<array size>]

To declare an array with initial values, follow

Syntax

<type> <array name> [<array size>] = {<value1>, <value2>, ...}

Usage of Arrays

Each array entry is a variable of the given type.
Useful in storing data in table forms
Array size must be a constant
The number of initial values cannot be larger than the array size.
Do not read from or write to a non-existing entry (e.g. x[6] in interger_array.cpp). Program will behave unpredictably.

For example, properties of 3 spheres can be stored in arrays each of 3 elements.

SphereProperties-array.cpp

// Properties of spheres of radii 1, 3, and 7 using arrays
#include <iostream>
#include <math.h>
using namespace std;
const double pi = 3.1416;
const int N=3; // no. of spheres
double r[N] =   {1., 3., 7.}; // array for radii of spheres

int main()  
{
  double area[N], volume[N]; // arrays for area and volume

  for (int i=0; i<N; ++i){
    area[i] = 4. * pi * pow(r[i], 2.);
    volume[i] = 4./3. * pi * pow(r[i], 3.);
    cout << r[i] << ' ' << area[i] << ' ' << volume[i] << endl;
  }
}

( SphereProperties-array.cpp )

Example: Maximum value
Find the maximum value in the sequence {15.1, 33., 0.3, 42.5, 8.8}

maximum.cpp

#include <iostream>
#include <math.h>
using namespace std;

const int n = 5; // array size
double x[n] = {15.1, 33., 0.3, 42.5, 8.8}; // array of doubles

int main()
{
  double x_max = x[0]; // max. of x initialized by entry 0

  for (int i=1; i<n; ++i){ // go through every other entry 
    if (x[i] > x_max)      // entry i > current maximum?
      x_max = x[i];        // replace current maximum 
  }
  cout << x_max << endl;
}

( maximum.cpp )

7.2 Two-dimensional Arrays

A two-dimensional array can store a table of numbers for further processing, e.g.

array2d.cpp

#include <iostream>
#include <math.h>
using namespace std;

const int nrow = 2; // number of rows
const int ncol = 3; // number of columns
int z[nrow][ncol] = { {1, 2, 3}, {4, 5, 6} };
  // 2d array of size nrow * ncol

int main()
{
  for (int i=0; i<nrow; ++i){
    for (int j=0; j<ncol; ++j){
      cout << z[i][j] << ' '; // output an array entry
    }
    cout << endl; // endline after last entry of a row
  }
}

( array2d.cpp )

The output is

1 2 3 
4 5 6

7.3 Further example

Example: Center of Mass
Four particles of the same mass are located at positions (0,0,6), (1,5,2), (3,3,3) and (5,2,6). Find the position of their center of mass.

The following program uses 3 one-dimensional arrays:

center-of-mass.cpp

#include <iostream>
#include <math.h>
using namespace std;

const int n=4; // no. of particles
double x[n] = {0., 1., 3., 5}; // coordinates of particles
double y[n] = {0., 5., 3., 2};
double z[n] = {6., 2., 3., 6};

int main(){
  double xsum=0, ysum=0, zsum=0; // sum of coordinates
  for (int i=0; i<n; ++i){
    xsum += x[i];
    ysum += y[i];
    zsum += z[i];
  }
  double xc = xsum/n;  // position of center of mass
  double yc = ysum/n;
  double zc = zsum/n;
  cout << xc << ' ' << yc << ' ' << zc << endl;
}

( center-of-mass.cpp )

Alternative, we can use a two-dimensional array:

center-of-mass2.cpp

#include <iostream>
#include <math.h>
using namespace std;

const int dim=3; // dimension
const int n=4; // no. of particles
double r[n][dim] = { {0,0,6},{1,5,2},{3,3,3},{5,2,6} }; // coordinates

int main(){
  double rsum[dim]; // sum of coordinates
  double rc[dim];   // position of center of mass 

  for (int u=0; u<dim; ++u){ // u-th dimension
    rsum[u]=0;
    for (int i=0; i<n; ++i){ // i-th particle
      rsum[u] += r[i][u];
    }
    rc[u] = rsum[u]/n;  // position of center of mass 
    cout << rc[u] << ' ';
  }
  cout << endl;
}

( center-of-mass2.cpp )

7.4 Initialization of Array without specifying size

Array with initial values need not specify size explicitly, i.e.

Syntax

<type> <array name> [] = {<value1>, <value2>, ...}

e.g.

double x[ ] = {15.1, 33., 0.3, 6.5, 8.8}; // array of doubles

The size automatically equals the number of values given, i.e. 5 in this example.

7.5 Strings

A C++ string is an array of char (characters).

char_string.cpp

#include <iostream>
#include <math.h>
using namespace std;

int main()
{
  char str[ ]="Hello"; // declare and initialize string
                         // constant string enclosed by "... "
  cout << str << endl;  // output the whole string
  for (int i=0; i<5; ++i){
    cout << str[i] << endl;  // output the i-th character 
  }
}

( char_string.cpp )

Program output:

Hello

Explanation

A constant string is enclosed by " ... ", e.g. "Hello".
The string "Hello" has 6 characters (not 5!) because there is a hidden end of string character (i.e. null character, with ASCII code 0) at the end, i.e. "Hello" represents 'H' + 'e' + 'l' + 'l' + 'o' + '\0'.
the size of the char array must be large enough to hold the constant string.

7.6 String operations

Function strcpy(s1, s2) , i.e. string copy, copies the content of string s2 to string variable s1.

Function strcat(s1, s2), i.e. string concatenate, append the content of string s2 to string variable s1.

e.g.

string_operation.cpp

// determine if a number is positive
#include <iostream>
#include <math.h>
#include <string.h>
using namespace std;

const double x=5;

const char s1[30] = "x is ";
const char s_positive[] = "positive";
const char s_negative[] = "negative";
int main()
{
  char response[30];

  strcpy( response, s1 ); // copy s1 to response
  if (x>=0){
    strcat( response, s_positive ); // add s_positive to response
  }else{
    strcat( response, s_negative ); // add s_negative to response
  }

  cout << response << endl;
}

( string_operation.cpp )

Chapter 8
Input / Output

8.1 Standard Output Stream (cout)

e.g. outputing 1.2 to the screen:

cout << 1.2 << endl;

Explanation

cout is a C++ object (i.e. variable with special properties)
cout is the standard output stream for outputting to screen
the output operator " << " is used to supply values to cout for outputting
Requires '#include <iostream>'

8.2 Output manipulators

An output manipulator will control certain properties of the output stream.

1. endl

End the current line of output and start a new line for future outputs.

2. setprecision

To choose the number of significant figures for floating point output, e.g.

outputmanip.cpp

#include <math.h>
#include <iostream>
#include <iomanip>
using namespace std;

int main()
{
  cout << 10./3. << endl; // 6 significant figures by default
  cout << setprecision(3) << 10./3. << endl; // 3 significant figures
  cout << setprecision(15) << 10./3. << endl;
  cout << setprecision(20) << 10./3. << endl; // seeing machine errors
}

( setprecision.cpp )

Program output:

3.33333
3.33
3.33333333333333
3.3333333333333334814

(The digits 4814... are due to machine imprecision, i.e. machine errors.)

Explanation

setprecision(n) set all subsequent floating point numeric outputs to n significant figures.
Default (i.e. preset) value of n is 6.
Requires '#include <iomanip>'

3. setw

Setting the width of the output, e.g.

setw.cpp

#include <math.h>
#include <iostream>
#include <iomanip>
using namespace std;

const int nrow = 2, ncol = 3; 
double z[nrow][ncol] = { {1./3, 1./9., 3.}, {-1./11., 5., 6.} };

int main()
{
  for (int i=0; i<nrow; ++i){
    for (int j=0; j<ncol; ++j){
      cout << setw(12) << z[i][j] ; // output with width 12
    }
    cout << endl; 
  }
}

( setw.cpp )

Program output:

    0.333333    0.111111           3
  -0.0909091           5           6

Explanation

setw(n) set the next output to have a width n.
best for outputting tables
Requires '#include <iomanip>'

8.3 Standard Input Stream (cin)

e.g. read an integer x from the keyboard and output the value:

cin_x.cpp

#include <math.h>
#include <iostream>
using namespace std;

int main()
{
  int x;
  cout << "Please enter a integer x" << endl;

  cin >> x; // reading a integer from keyboard and assign to x

  cout << "x = " << x << endl;
}

( cin_x.cpp )

Program output, given that the user typed in the value 135:

Please enter an integer x
135
x = 135

Explanation

cin is a C++ object
cin is the standard input stream for reading from the keyboard
the input operator " >> " is used to direct input values to variables
user input is echoed (i.e. repeated) on the screen
input value must be followed by the key "enter" to end the input
non-integer input in general will give unpredictable result (not recommended)

e.g. reading two doubles from the keyboard and output their sum:

cin_sum.cpp

#include <math.h>
#include <iostream>
using namespace std;

int main()
{
  double x, y;
  cin >> x >> y; // reading two doubles 
  double sum = x + y;
  cout << sum << endl;
}

( cin_sum.cpp )

Explanation

a cin statement can involves two or more input operators ">>"
the first value will be assigned to x, and the second to y
the two inputs can be separated by the "enter" key, or by a space.
non-numeric values (e.g. "abc") in general will give unpredictable result (not recommended)

8.4 Is input successful?

The input operation gives a boolean value on whether input is successful.

cin_check.cpp

#include <math.h>
#include <iostream>
using namespace std;

int main()
{
  double x;
  if (cin >> x)  // check whether input is successful
    cout << "x = " << x << endl; // input successful
  else
    cout << "invalid input" << endl; // input failed
}

( cin_check.cpp )

Output, e.g. with input '135':

135
x = 135

e.g. with input 'abc'

abc
invalid input

A popular use is to a variable number of read input values until an invalid input is entered.

e.g. to read an arbitrary number of floating point numbers and output the sum:

cin_loop.cpp

#include <math.h>
#include <iostream>
using namespace std;

int main()
{
  double x, sum=0;
  cout << "Please input numerical values, ended by a <Control-D>" << endl;

  while (cin >> x){ // repeat while reading is successful
    cout << "input = " << x << endl;
    sum += x;       // add number to sum
  }
  cout << "sum = " << sum << endl;
}

( cin_loop.cpp )

Output (with user inputing 3.14 <enter> 5 <enter> <Control-D>):

Please input numerical values, ended by a <Control-D>
3.14
input = 3.14
5
input = 5
sum = 8.14

Explanation

Loop as long as 'cin >> x' returns true, indicating successful reading.
Looping stops when user inputs invalid value (e.g. "abc"), or a <Control-D> (i.e., an end-of-text character, ASCII code 4).

8.5 File Output

e.g.

file_output.cpp

// output the result of x + y into a file 'sum.txt'
#include <math.h>
#include <iostream>
#include <fstream>
using namespace std;

const int x = 5, y = 11;
int main()
{
  ofstream outfile("sum.txt");// open output file sum.txt
  outfile << x + y << endl;   // output to file
  outfile.close();            // close file
}

( file_output.cpp )

The output file is sum.txt

Explanation

Requires '#include <fstream>'
ofstream (i.e. output file stream) is an advanced C++ data type.
ofstream <stream name>(" < file name > ") does the following
- declares an ofstream variable of name <stream name> (e.g. outfile)
- associate <file name> (e.g. sum.txt) with the output file stream
- open the file for output
the output operator, << outputs values to the output file stream.
outfile.close() closes the file and finishes outputting.
A filename extension 'txt' usually denotes text file format and can be opened by e.g. microsoft notepad.

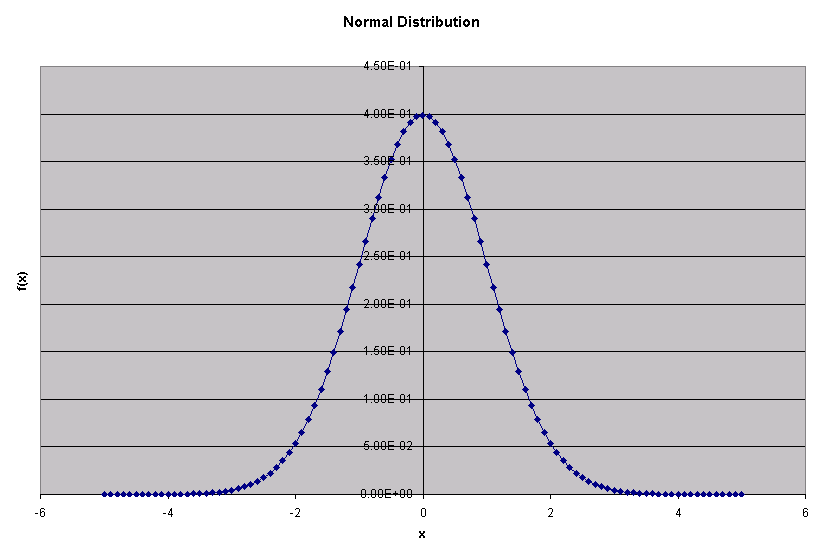
e.g. calculate a table of values for the normal distribution function defined by

f(x) =

√

2π

e^−x²/2

for x=−5, −0.49, −0.48, ... 5.

normal_dist.cpp

// output a table of values for the normal distribution function
#include <math.h>
#include <iostream>
#include <fstream>
using namespace std;

const double pi=3.1416;

double f(double x){
  return (1./sqrt(2*pi))*exp( -x*x/2. );
}

int main()
{
  ofstream ofile("normal.csv"); // open file for output

  for (double x=-5.; x<=5.; x+=0.01) // go over many values of x in [-5,5]
    ofile << x << ", " << f(x) << endl;     // output to file

  ofile.close();              // close file
}

( normal_dist.cpp )

The output file is normal.csv.

Explanation

A filename extension 'csv' usually denotes comma separated value file format which can be opened by e.g. microsoft excel, or microsoft notepad.

8.6 Graph Plotting

After executing normal_dist.cpp following the procedure in Sec. , we can plot a graph using the data file normal.csv as follows

Access the file using the window explorer by clicking Start - - > My Documents - - > Visual Studio 2008 - - > Project - - > normal_dist - - > normal_dist
Click normal.csv (which may only be displayed as normal) to open it with Microsoft Excel. If Excel does not start, right click normal.csv and click Open With - - > Mirosoft Excel
In Excel, press Control-A to highlight the whole spreadsheet.
Click Insert - - > Chart - - > XY (Scatter)
On the Chart sub-type pane, click the one described as Scatter with data points connected by lines
Click Next - - > Next - - > Next - - > Finish

After adding title, and x-y labels, we get a graph like this

8.7 File Input

The file normal.csv is convenient for working with Microsoft Excel. Alternatively, omitting the comma in normal_dist.cpp, results can be output as a plain-text data file normal.txt.

normal.txt can be read by the following program

file_input.cpp

// read a table of values written by normal_dis.cpp
#include <math.h>
#include <iostream>
#include <fstream>
using namespace std;

int main()
{
  ifstream infile("normal.txt"); // open file for input

  double x, f;
  while (infile >> x){ // loop while reading is successful
    infile >> f;       // read f(x) 
    cout << x << ' ' << f << endl;  // output values to screen
  }
  infile.close();              // close file
}

( file_input.cpp )

Explanation

Requires '#include <fstream>'
ifstream denotes the input file stream data type
The data file normal.txt must first be copied to the current project folder.

Chapter 9
Developing larger programs

9.1 Ordering of functions

Example:
Calculate the sum of volume and mass of spheres of radii 1 and 3 and density 7.87.

Without function declarations:

SphereSum.cpp

// sum of volume and mass of spheres
#include <iostream>
#include <math.h>
using namespace std;

double volume(double r)
{
  const double pi = 3.1416;
  return 4./3. * pi * pow(r, 3.);
}

double mass(double r, double rho) // must be defined after volume()
{
  return rho * volume(r);
}

// main function

const double r1=1.; // radius of first sphere
const double r2=3.; // radius of first sphere
const double rho=7.87; // density

int main()  // must be defined after volume() and mass()
{
  double volume_sum = volume(r1) + volume(r2);
  cout << volume_sum << endl; // sum of volume

  double mass_sum = mass(r1, rho) + mass(r2, rho);
  cout << mass_sum << endl;  // sum of mass
}

( SphereSum.cpp )

Functions must be defined before used. Therefore,

mass() must be defined after volume();
main() must be defined after mass() and volume().

Disadvantage: Required order may disallow better ordering according to, e.g. the type of task performed by functions.

9.2 Function declarations

A function definition can include function declaration and function implementation

Syntax

// declaration
<return type> <func. name> ( [<vari. type> <vari. name>] [, ...] );

...

// implementation
<return type> <func. name> ( [<vari. type> <vari. name>] [, ...] ){
  statement
}

Explanation

A function can be used after declared.
Function declaration is optional.
Function declaration if exists must precede implementation.
The declaration must be consistent with implementation, i.e. same return type, argument types, etc.

e.g. with function declarations, mass() can be implemented before volume() :

SphereSum-func-declaration.cpp

// sum of volume and mass of spheres
#include <iostream>
#include <math.h>
using namespace std;

// function declarations
double mass(double r, double rho);
double volume(double r);

// function implementations

double mass(double r, double rho) 
{
  return rho * volume(r);
}

double volume(double r) 
{
  const double pi = 3.1416;
  return 4./3. * pi * pow(r, 3.);
}

// main function

const double r1=1.; // radius of first sphere
const double r2=3.; // radius of first sphere
const double rho=7.87; // density

int main()  
{
  double volume_sum = volume(r1) + volume(r2);
  cout << volume_sum << endl; // sum of volume

  double mass_sum = mass(r1, rho) + mass(r2, rho);
  cout << mass_sum << endl;  // sum of mass
}

( SphereSum-func-declaration.cpp )

9.3 Multiple C++ source files

Larger C++ programs are often split into multiple files.

Advantages

different tasks in separate files highlight software design structure,
functions in some files can be re-used in other applications
different people can work on different files more easily

e.g. the above program is split into :

SphereSum-main.cpp

// sum of volume and mass of spheres
#include <iostream>
#include <math.h>
using namespace std;

// function declaration (implementation in sphere.cpp)
double mass(double r, double rho);
double volume(double r);

// main function

const double r1=1.; // radius of first sphere
const double r2=3.; // radius of second sphere
const double rho=7.87; // density

int main()  
{
  double volume_sum = volume(r1) + volume(r2);
  cout << volume_sum << endl; // sum of volume

  double mass_sum = mass(r1, rho) + mass(r2, rho);
  cout << mass_sum << endl;  // sum of mass
}

( SphereSum-main.cpp )

Sphere.cpp

// functions for properties of sphere
#include <iostream>
#include <math.h>
using namespace std;
const double pi = 3.1416;

// function declarations
double mass(double r, double rho);
double volume(double r);

// function implementations

double mass(double r, double rho) 
{
  return rho * volume(r);
}

double volume(double r) 
{
  const double pi = 3.1416;
  return 4./3. * pi * pow(r, 3.);
}

( Sphere.cpp )

Explanation

splitting allows Sphere.cpp, which is very general, to be reused in other applications
Only one source file should contain main()
Functions used in a source file must be defined or declared in the same file before use.

9.4 C++ Header file and Include statement

A deficiency in the above programs (i.e. SphereSum-main.cpp and Sphere.cpp) is that function declarations appear twice in both files. Modification of function declarations can be troublesome.

Solution: Create a header file with filename extension "h", i.e.

sphere.h contains function declarations.
sphere.cpp contains function implementations
Spheresum2.cpp uses functions in sphere.cpp

sphere.h

// sphere.h (header file for sphere.cpp)
double mass(double r, double rho);
double volume(double r);

( sphere.h )

sphere.cpp

// sphere.cpp : functions for properties of sphere
#include <iostream>
#include <math.h>
#include "sphere.h" // include header file

using namespace std;
const double pi = 3.1416;

// function implementations

double mass(double r, double rho) 
{
  return rho * volume(r);
}

double volume(double r) 
{
  const double pi = 3.1416;
  return 4./3. * pi * pow(r, 3.);
}

( sphere.cpp )

SphereSum2.cpp

// sum of volume and mass of spheres
#include <iostream>
#include <math.h>
#include "sphere.h" // include header file 

using namespace std;

// main function

const double r1=1.; // radius of first sphere
const double r2=3.; // radius of second sphere
const double rho=7.87; // density

int main()  
{
  double volume_sum = volume(r1) + volume(r2);
  cout << volume_sum << endl; // sum of volume

  double mass_sum = mass(r1, rho) + mass(r2, rho);
  cout << mass_sum << endl;  // sum of mass
}

( SphereSum2.cpp )

"include" statement

#include "sphere.h" tells the compiler to replace this line by the content of the file sphere.h.
The file sphere.h should be located at the same folder as other source files.
include <math.h> tells the compiler to replace this line by the content of the file math.h located at the usual header file folder. For example, math.h is located at folder C:\Program Files\Microsoft Visual Studio 9.0\VC\include.

To create the header file sphere.h in Visual C++, do the following (see also Section 2.2)

In Solution Explorer, highlight "Source Files".
Click Project menu - - > Add New Item.
In the Add New Item dialog box, select the "Header File (.h)" Template from the right pane.
Enter "sphere" for the Name of the source file and then click Add
In the new "sphere.h" tab, type in our C++ program source codes.

9.5 Namespace

Related variables and functions can be grouped into a namespace.

Syntax

namespace <name>
{
   <variable declaration>
   ... 

   <function definition> 
   ...
}

e.g. rewriting SphereSum.cpp using namespace:

SphereSum-ns.cpp

// sum of volume and mass of spheres
#include <iostream>
#include <math.h>
using namespace std;

namespace sphere
{
  double volume(double r)
  {
    const double pi = 3.1416;
    return 4./3. * pi * pow(r, 3.);
  }
  
  double mass(double r, double rho)
  {
    return rho * volume(r); // calling func. within the same namespace
  }
}

const double r1=1., r2=3.; // radii of spheres 
const double rho=7.87; // density

int main()  
{  
  // calling func. outside namespace
  double volume_sum = sphere::volume(r1) + sphere::volume(r2); 
  cout << volume_sum << endl; // total volume

  double mass_sum = sphere::mass(r1, rho) + sphere::mass(r2, rho);
  cout << mass_sum << endl;  // total mass
}

( SphereSum-ns.cpp )

Explanation

Within the namespace, a function can be used just like before, e.g. calling volume() in mass().
Outside the namespace, a function is called by <namespace>::<function name>, e.g sphere::volume() in main().

Applying the using <namespace> statement, "<namespace>::" can be omitted, e.g.

SphereSum-ns2.cpp

// sum of volume and mass of spheres
#include <iostream>
#include <math.h>
using namespace std;

namespace sphere
{
  double volume(double r)
  {
    const double pi = 3.1416;
    return 4./3. * pi * pow(r, 3.);
  }
  
  double mass(double r, double rho)
  {
    return rho * volume(r); 
  }
}

const double r1=1., r2=3.; // radii of spheres 
const double rho=7.87; // density

int main()  
{  
  using namespace sphere;

  double volume_sum = volume(r1) + volume(r2); // sphere:: omitted 
  cout << volume_sum << endl; // total volume

  double mass_sum = mass(r1, rho) + mass(r2, rho);
  cout << mass_sum << endl;  // total mass
}

( SphereSum-ns2.cpp )

Functions with identical names can be defined in different namespaces.

Example:
Calculate the total mass of a cube of length 1 and a sphere of radius 2 both having a density 7.87.

CubeSphere.cpp

// total mass of cube and sphere
#include <iostream>
#include <math.h>
using namespace std;

namespace cube
{
  double volume(double l)
  {
    return pow(l, 3.);
  }
  
  double mass(double l, double rho)
  {
    return rho * volume(l); 
  }
}

namespace sphere
{
  double volume(double r)
  {
    const double pi = 3.1416;
    return 4./3. * pi * pow(r, 3.);
  }
  
  double mass(double r, double rho)
  {
    return rho * volume(r); 
  }
}

const double rho=7.87; // density

int main()  
{  
  double mass_sum = cube::mass(1., rho) + sphere::mass(2., rho);
  cout << mass_sum << endl; 
}

( CubeSphere.cpp )

File translated from T_EX by T_TH, version 4.06.
On 7 Jan 2019, 11:31.

C++ programming for beginning programmers

Contents

Chapter 1 Overview of C++

1.1 The simplest C++ program

1.2 Execute C++ Program Online

1.3 Mathemical functions

1.4 Comments in a program

1.5 Microsoft Visual Studio

1.6 Using variables

1.7 If and else

1.8 Program indentation

1.9 While loop

1.10 Debugging approaches

Chapter 2 C++ Fundamental Data Types

2.1 Integer

2.2 Floating point number

2.3 Boolean

2.4 Character

Chapter 3 Identifier and Variable

3.1 Identifier

3.2 Variable Declaration

3.3 Scope of Variable

Chapter 4 Operators and Expressions

4.1 Assignment operator (=)

4.2 Arithmetic operators (+, - ,* , / , %)

4.3 Compound assignment( +=, -=, *=, /=, %= )

4.4 increase operator (++) and decrease operator (- -)

4.5 Equality and Relational operators ( ==, !=, >, <, >=, <= )

4.6 Logical operators ( !, &&, | | )

4.7 Precedence of operators

Chapter 5 Program control statements

5.1 Simple statement and block of statements

5.2 If and else

5.3 While loop

5.4 For loop

5.5 Nested loops

5.6 Further example

Chapter 6 Functions

6.1 Function Definition and Usage

6.2 Value as Argument of function

6.3 Returned value of function

6.4 Mathematical Functions

6.5 Variable as Argument of Function

Chapter 7 Arrays

7.1 Array Declaration and Usage

7.2 Two-dimensional Arrays

7.3 Further example

7.4 Initialization of Array without specifying size

7.5 Strings

7.6 String operations

Chapter 8 Input / Output

8.1 Standard Output Stream (cout)

8.2 Output manipulators

8.3 Standard Input Stream (cin)

8.4 Is input successful?

8.5 File Output

8.6 Graph Plotting

8.7 File Input

Chapter 9 Developing larger programs

9.1 Ordering of functions

9.2 Function declarations

9.3 Multiple C++ source files

9.4 C++ Header file and Include statement

9.5 Namespace

Chapter 1
Overview of C++

Chapter 2
C++ Fundamental Data Types

Chapter 3
Identifier and Variable

Chapter 4
Operators and Expressions

Chapter 5
Program control statements

Chapter 6
Functions

Chapter 7
Arrays

Chapter 8
Input / Output

Chapter 9
Developing larger programs